《Attention is All you need》论文解读

AI人工智能, Python, 架构设计, 算法 / 作者： / / 发表评论 / Attention is All you need, Attention机制, Decoder, Encoder, length path, Position Embedding, Position-wise Feed-forward Networks, Transformer Architecture, Why Self-Attention, 并行计算, 相关程度, 计算复杂度分析

Attention机制最早在视觉领域提出，2014年Google Mind发表了《Recurrent Models of Visual Attention》，使Attention机制流行起来，这篇论文采用了RNN模型，并加入了Attention机制来进行图像的分类。

2015年，Bahdanau等人在论文《Neural Machine Translation by Jointly Learning to Align and Translate》中，将attention机制首次应用在nlp领域，其采用Seq2Seq+Attention模型来进行机器翻译，并且得到了效果的提升，Seq2Seq With Attention中进行了介绍。

2017 年，Google 机器翻译团队发表的《Attention is All You Need》中，完全抛弃了RNN和CNN等网络结构，而仅仅采用Attention机制来进行机器翻译任务，并且取得了很好的效果，注意力机制也成为了大家近期的研究热点。该论文发表在NIPS 2017上。

一、Attention机制

Attention用于计算”相关程度“，例如在翻译过程中，不同的英文对中文的依赖程度不同，Attention通常可以进行如下描述，表示为将query(Q)和key-value pairs

$$\{K_i, V_i | i=1,2,\ldots,m\}$$

映射到输出上，其中query、每个key、每个value都是向量，输出是V中所有values的加权，其中权重是由Query和每个key计算出来的，计算方法分为三步。

1、计算方法三步

1）第一步

第一步：计算比较Q和K的相似度，用f来表示：

$$f(Q, K_i), i=1,2, \ldots, m \tag{1}$$

2）第二步

第二步：将得到的相似度进行Softmax操作，进行归一化：

$$\alpha_i=\frac{e^{f(Q, K_i)}}{\sum_{j=1}^{m}f(Q, K_j)}, i = 1, 2,\ldots, m\tag{2}$$

3）第三步

第三步：针对计算出来的权重αi，对V中所有的values进行加权求和计算，得到Attention向量：

$$\sum_{i=1}^{m}\alpha_i, V_i\tag{3}$$

2、第一步的计算方法

通常第一步中计算方法包括以下四种：

1）点乘 dot product

$$f(Q, K_i)=Q^TK_i\tag{4}$$

2）权重 General

$$f(Q, K_i)=Q^TWK_i\tag{5}$$

3）拼接权重 Concat

$$f(Q, K_i)=W\left[Q;K_i\right]\tag{6}$$

4）感知器 Perceptron

$$f(Q, K_i)=V^Ttanh(WQ+UK_i)\tag{7}$$

二、Transformer Architecture

绝大部分的序列处理模型都采用encoder-decoder结构，其中encoder将输入序列

$$(x_1,x_2,\ldots,x_n)$$

映射到连续表示

$$\vec{z}=(z_1,z_2, \ldots ,z_n)$$

然后decoder生成一个输出序列

$$(y_1,y_2,\ldots,y_m)$$

每个时刻输出一个结果。Transformer模型延续了这个模型，整体架构如下图1所示：

《Attention is All you need》论文解读插图
图1 基于Transformer模型的Encoder-Decoder模型示意图

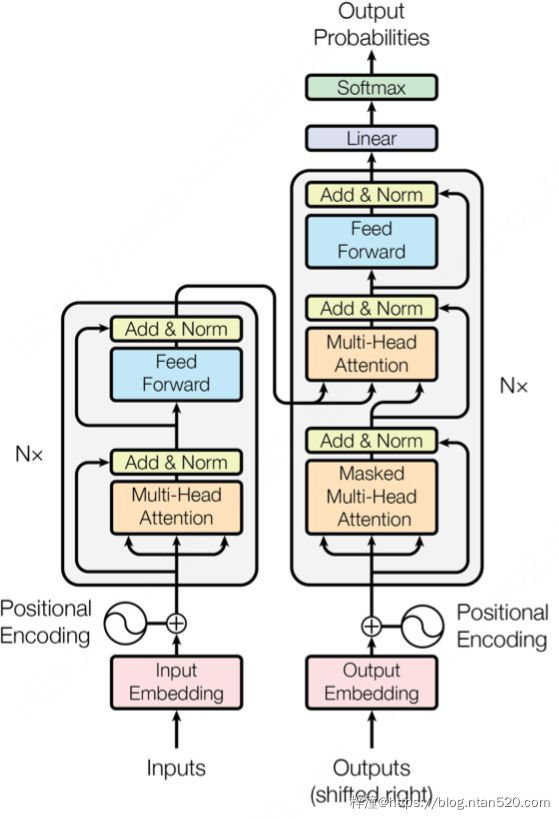
1、Encoder

Encoder有N=6层，每层包括两个sub-layers：

  • 1. 第一个sub-layer是multi-head self-attention mechanism，用来计算输入的self-attention
  • 2. 第二个sub-layer是简单的全连接网络。

在每个sub-layer我们都模拟了残差网络，每个sub-layer的输出都是

$$LayerNorm(x+Sublayer(x))\tag{8}$$

其中Sublayer(x) 表示Sub-layer对输入 x 做的映射，为了确保连接，所有的sub-layers和embedding layer输出的维数都相同：

$$d_{model}=512$$

2、Decoder

Decoder也是N=6层，每层包括3个sub-layers：

  • 1. 第一个是Masked multi-head self-attention，也是计算输入的self-attention，但是因为是生成过程，因此在时刻 i 的时候，大于 i 的时刻都没有结果，只有小于 i 的时刻有结果，因此需要做Mask
  • 2. 第二个sub-layer是全连接网络，与Encoder相同
  • 3. 第三个sub-layer是对encoder的输入进行attention计算。

同时Decoder中的self-attention层需要进行修改，因为只能获取到当前时刻之前的输入，因此只对时刻 t 之前的时刻输入进行attention计算，这也称为Mask操作。

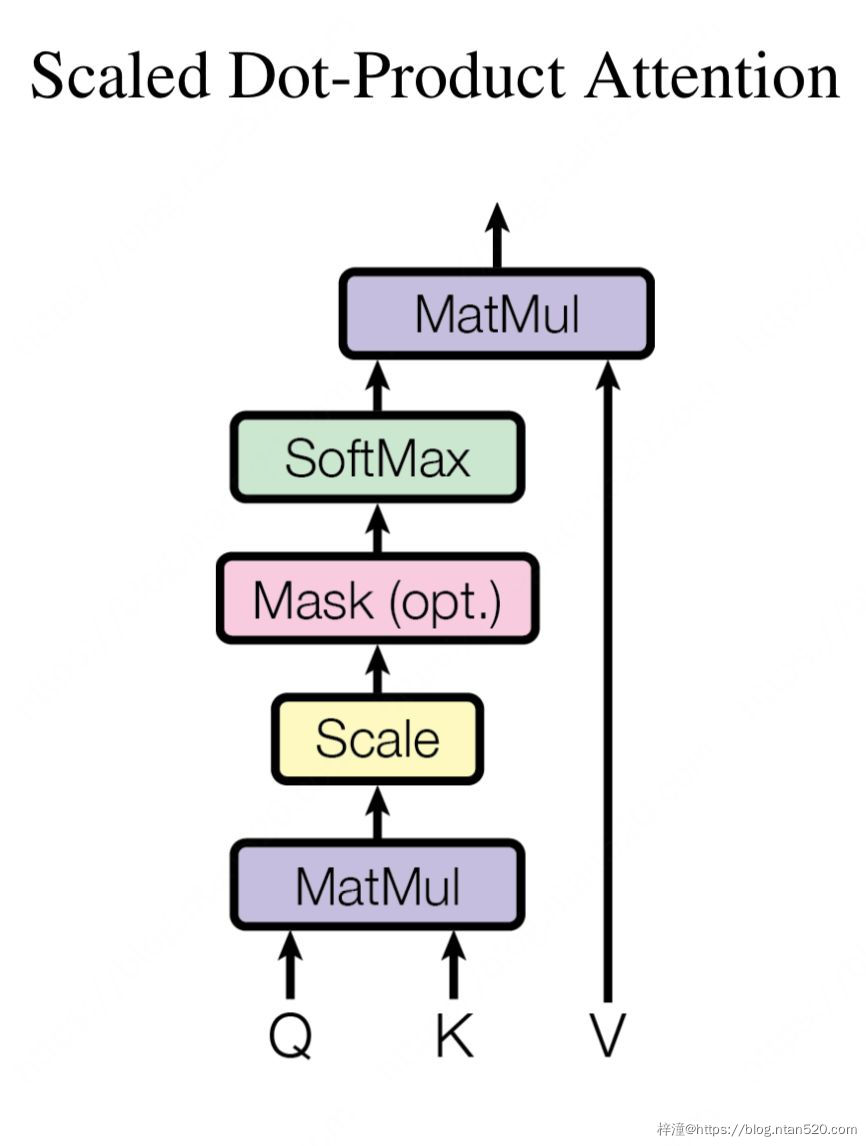
3、Attention机制

在Transformer中使用的Attention是Scaled Dot-Product Attention, 是归一化的点乘Attention，假设输入的query q 、key维度为 dk ,value维度为 dv , 那么就计算query和每个key的点乘操作，并除以《Attention is All you need》论文解读插图2 ，然后应用Softmax函数计算权重。

$$Attention(Q,K_i,V_i)=softmax(\frac{Q^TK_i}{\sqrt{d_k}})V_i\tag{9}$$

在实践中，将query和keys、values分别处理为矩阵 Q,K,V , 那么计算输出矩阵为：

$$Attention(Q,K,V)=softmax(\frac{Q^TK}{\sqrt{d_k}})V\tag{10}$$

其中 

$$Q \in R^{m \times d_k}$$
$$K \in R^{m \times d_k}$$
$$V \in R^{m \times d_v}$$

输出矩阵维度为

$$R^{m \times d_v}$$

如下所示

$$ Q= \underbrace{ \begin{pmatrix} q \\ q \\ q \\ \vdots \\ q \\ \end{pmatrix}}_{d_k}\quad \}m\tag{11}$$
$$ K= \underbrace{ \begin{pmatrix} k_1 \\ k_2 \\ k_3 \\ \vdots \\ k_m \\ \end{pmatrix}}_{d_k}\quad \}m\tag{12}$$
$$ V= \underbrace{ \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ \vdots \\ v_m \\ \end{pmatrix}}_{d_v}\quad \}m\tag{13}$$

那么Scaled Dot-Product Attention的示意图如下所示，Mask是可选的(opt.)，如果是能够获取到所有时刻的输入(K, V), 那么就不使用Mask；如果是不能获取到，那么就需要使用Mask。使用了Mask的Transformer模型也被称为Transformer Decoder，不使用Mask的Transformer模型也被称为Transformer Encoder。

《Attention is All you need》论文解读插图4
图2 Scaled Dot-Product Attention示意图

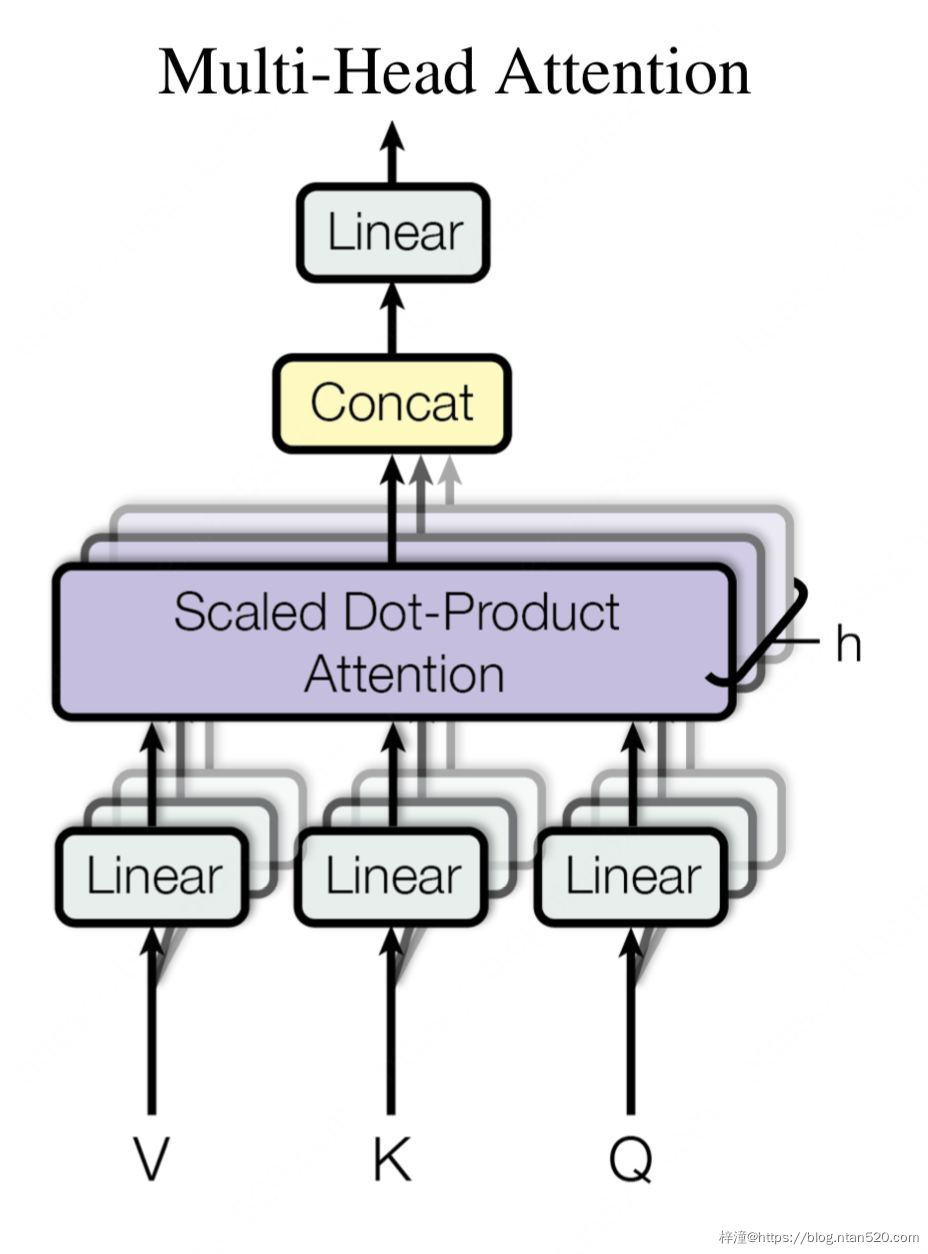
如果只对Q、K、V做一次这样的权重操作是不够的，这里提出了Multi-Head Attention，操作包括：

  • 1. 首先对Q、K、V做一次线性映射，将输入维度均为 dmodel 的 Q,K,V 矩阵映射到 Q∈Rm×dk , K∈Rm×dk  , V∈Rm×dv 
  • 2. 然后在采用Scaled Dot-Product Attention计算出结果
  • 3. 多次进行上述两步操作，然后将得到的结果进行合并
  • 4. 将合并的结果进行线性变换

总结来说公示如下所示：

$$\begin{align*} Attention(Q,K,V)=Concat(head_1, head_2, \ldots , head_h) W^O \\ wherehead_i = Attention(QW_i^Q, KW_i^K, VW_i^V) \end{align*} \tag{14}$$

其中第1步的线性变换参数为：

$$W_i^Q \in R^{d_{model} \times d_k}$$
$$W_i^K \in R^{d_{model} \times d_k}$$
$$W_i^V \in R^{d_{model} \times d_v}$$

第4步的线性变化参数为：

$$W^O \in R^{hd_v \times d_{model}}$$

而第三步计算的次数是 h。

在论文中取 dmodel=512, 表示每个时刻的输入维度和输出维度， ℎ=8 表示8次Attention操作，dk = dv = dmodel / h = 64 表示经过线性变换之后、进行Attention操作之前的维度。那么进行一次Attention之后输出的矩阵维度是 Rm x dv = Rm x 64 , 然后进行h = 8次操作合并之后输出的结果是 Rm×(ℎ×dv) = Rm×512 ，因此输入和输出的矩阵维度相同。

这样输出的矩阵 Rm×512 ，每行的向量都是对 V 向量中每一行 vi 的加权，示意图如下所示：

《Attention is All you need》论文解读插图6
图3 Multi-Head Attention机制示意图

在图1的Encoder-Decoder架构中，有三处Multi-head Attention模块，分别是：

  • 1. Encoder模块的Self-Attention，在Encoder中，每层的Self-Attention的输入 Q=K=V , 都是上一层的输出。Encoder中的每个position都能够获取到前一层的所有位置的输出。
  • 2. Decoder模块的Mask Self-Attention，在Decoder中，每个position只能获取到之前position的信息，因此需要做mask，将其设置为 −∞
  • 3. Encoder-Decoder之间的Attention，其中 Q 来自于之前的Decoder层输出， K,V 来自于encoder的输出，这样decoder的每个位置都能够获取到输入序列的所有位置信息。

4、Position-wise Feed-forward Networks

在进行了Attention操作之后，encoder和decoder中的每一层都包含了一个全连接前向网络，对每个position的向量分别进行相同的操作，包括两个线性变换和一个ReLU激活输出：

$$FFN(x)=max(0, xW_1 \times b_1)W_2 \times b_2 \tag{15}$$

其中每一层的参数都不同。

5、Position Embedding

因为模型不包括recurrence/convolution，因此是无法捕捉到序列顺序信息的，例如将K、V按行进行打乱，那么Attention之后的结果是一样的。但是序列信息非常重要，代表着全局的结构，因此必须将序列的token相对或者绝对position信息利用起来。

这里每个token的position embedding 向量维度也是 dmodel = 512，然后将原本的input embedding和position embedding加起来组成最终的embedding作为encoder/decoder的输入。其中position embedding计算公式如下：

$$ \begin{align*} PE_{(pos, 2i)} = sin( pos / 10000^{ 2i / d_{model}}) \\ PE_{(pos, 2i + 1)} = cos( pos / 10000^{ 2i / d_{model}}) \end{align*} \tag{16} $$

其中 pos 表示位置index， i 表示dimension index。

Position Embedding本身是一个绝对位置的信息，但在语言中，相对位置也很重要，Google选择前述的位置向量公式的一个重要原因是：由于我们有

$$ \begin{align*} sin(\alpha + \beta) = sin \alpha \times cos \beta + cos \alpha \times sin \beta \\ cos(\alpha + \beta) = cos \alpha \times cos \beta – sin \alpha \times sin \beta \end{align*} \tag{17} $$

这表明位置p+k的向量可以表示成位置p的向量的线性变换，这提供了表达相对位置信息的可能性。

在其他NLP论文中，大家也都看过position embedding，通常是一个训练的向量，但是position embedding只是extra features，有该信息会更好，但是没有性能也不会产生极大下降，因为RNN、CNN本身就能够捕捉到位置信息，但是在Transformer模型中，Position Embedding是位置信息的唯一来源，因此是该模型的核心成分，并非是辅助性质的特征。

也可以采用训练的position embedding，但是试验结果表明相差不大，因此论文选择了sin position embedding，因为

  • 1. 这样可以直接计算embedding而不需要训练，减少了训练参数。
  • 2. 这样允许模型将position embedding扩展到超过了training set中最长position的position，例如测试集中出现了更大的position，sin position embedding依然可以给出结果，但不存在训练到的embedding。

三、Why Self-Attention

这里将Self-Attention layers和recurrent/convolutional layers来进行比较，来说明Self-Attention的好处。假设将一个输入序列

$$(x_1,x_2, \ldots ,x_n)$$

分别用

  • 1. Self-Attention Layer
  • 2. Recurrent Layer
  • 3. Convolutional Layer

来映射到一个相同长度的序列

$$(z_1,z_2,\ldots,z_n)$$

其中

$$x_i, z_i \in R^d $$

我们分析下面三个指标：

  • 1. 每一层的计算复杂度
  • 2. 能够被并行的计算，用需要的最少的顺序操作的数量来衡量
  • 3. 网络中long-range dependencies的path length，在处理序列信息的任务中很重要的在于学习long-range dependencies。影响学习长距离依赖的关键点在于前向/后向信息需要传播的步长，输入和输出序列中路径越短，那么就越容易学习long-range dependencies。因此我们比较三种网络中任何输入和输出之间的最长path length

结果如下所示：

《Attention is All you need》论文解读插图8

1、并行计算

Self-Attention layer用一个常量级别的顺序操作，将所有的positions连接起来

Recurrent Layer需要 O(n) 个顺序操作

2、计算复杂度分析

如果序列长度 n< 表示维度 d ，Self-Attention Layer比recurrent layers快，这对绝大部分现有模型和任务都是成立的。

为了提高在序列长度很长的任务上的性能，我们对Self-Attention进行限制，只考虑输入序列中窗口为 r 的位置上的信息，这称为Self-Attention(restricted), 这回增加maximum path length到 O(n/r) .

3、length path

如果卷积层kernel width k<n ，并不会将所有位置的输入和输出都连接起来。这样需要 O(n/k) 个卷积层或者 O(logk(n)) 个dilated convolution，增加了输入输出之间的最大path length。

卷积层比循环层计算复杂度更高，是k倍。但是Separable Convolutions将见效复杂度。

同时self-attention的模型可解释性更好(interpretable)。

四、Reference

打赏微海报分享

相关文章

发表评论